Partial orders can also have maximums
196
Be sure to follow the rule before you head out.
Rule: You must post before you leave.
If you have any questions, feel free to contact us on our matrix channel.
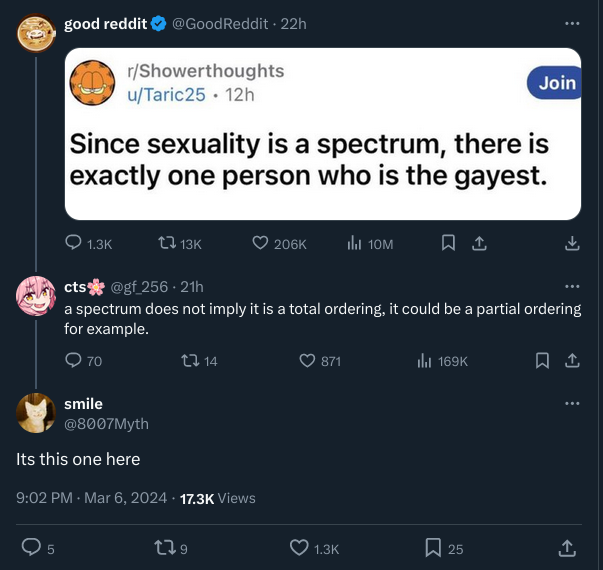
But maximums are only guaranteed to be represented by a unique element in in total orderings.
Edit: also, infinite sets might not necessarily contain an element of their maximum value.
There are demonstrably not infinite humans alive at the same time though.
Find the local maximum by taking the derivative:
dgay
dt
Sexuality has multiple axes.
- Intensity
- Orientation (towards Men, Women, Frogs)
- Time (people have been known to have straight periods, gay periods, horny periods, ace periods, etc.)
There are probably others that we relate to kink and paraphilia.
So the very gayest person would have to be specifically defined. Which is gayer: the horniest bisexual or the average-libido gay who has absolute-zero-Kelvin interest in the other sex? Or the gay man who is totally in love with (and exclusively devoted to) his hubby and has been this way for fifty years?
The gay agenda's got axes now?
Turning the frogs gay and then giving them axes!!
Comment sections like this make me feel like I'm in a room full of crazy people, and or I eventually start to question my own sanity.
I mean sure, a spectrum is defined by at least 2 most extreme points (depending on the amount of dimensions). But like, what's stopping us form mapping two or more people to either extreme? Why can't 2 people be equally most gay or equally least gay?
If you limit the resolution of the gayness measurement, sure. You could define least gay as 0 and most gay as 5, then you have millions of people on 5. But there are infinitely many real numbers, and if there were some theoretical 100% accurate way to measure "gayness" (whatever that means) at "infinite resolution", the chance of two people being equally most gay is theoretically 0. On the other hand of the spectrum, it'd be impossible to be ENTIRELY not gay at all, so even if millions of people are very close to 0, one would be the closest.
I'm way overthinking this lol
Number theory suggests that by whatever metric it's determined, there's bound to be an infinitesimal difference between two measurements. Observation leads to significant figures, not reality
Well that depends on if gayness is a continuous or discrete quantity. If gay comes in very small but distinct indivisible units, the minimum could certainly be just 1 of these units.
Still, the upper range is likely to be unbound.
I don't think there's such a thing as a discrete gay.. number and the sofar unmentioned bi spectrum implies a distributed or Cartesian system of expression
I think that could be possible. If sexuality were multi-dimensional and "gayness" was just a 1-D collapse of a higher dimensional space then you could pick a vector in the higher dimensional space to represent gayness, such that a few points at the extreme happen to have the same dot-product with that vector.
But then you would be defining gayness around the gymnastics of setting that up instead of something you are actually trying to estimate about people on that spectrum.
How is a spectrum supposed to not have a total ordering? To me saying sth is a spectrum always invokes an image of being able to map to/represent the property as an interval (unbounded or bounded) which should always give it a total ordering right?
How is a spectrum supposed to not have a total ordering?
I'm pretty sure a spectrum is always totally ordered. You can't say "this point on the spectrum holds no relation to that point", because then it's not a spectrum.
Only 1D spectrums. In 2D spectrums there's only a maximum relative to a specific 1D projection
It all comes down to definitions. First off, Totally Ordered is a property of the function that compares two elements not the set you are talking about. most sets have total orderings (if the axiom of choice is true then all sets have a total ordering). With Fields and vectorspaces there is the concept of a totally ordered Field which is essentially when the total ordering is compatible with it's field operations (e.g the set of complex numbers has many total orderings, but the field of complex numbers is not an ordered field).
So it really depends on how we define the sexuality spectrum. So long as it's simply a set then it has a total ordering. But if we allow us to add and multiply the gays then depending on how we define those functions it could be impossible to order the gay field.
Also a total ordering doesn't mean that there is exactly 1 maximal element (it would need to be a strict total ordering to have that property), so we can all be the gayest.
Now I'm wondering what the gayest gay person would look like.

Since the real numbers are a spectrum there exists one number which is the largest
Not comparable. There are finite gay people but infinite real numbers
Found him again
You have ignored the possibility that even though there are finite gay people, among those finite gays one of them might be infini-gay.
There's still gay people on Xitter? Why? It's full of Nazis.
Every large social platform has groups of people who hate each other, even lemmy. They just all have ways to keep only showing people the posts from groups they support (through defederation and only looking at specific communities, or twitter/youtube/tiktok/facebook's algorithms, etc)
plenty of gay furry artists around on that platform making lots of gay furry porn
Awsome logic in the original original post.
On a totally unrelated note: whats the biggest number between 0 and 1 (0<x<1)?
The set of all living humans is finite, so (if sexuality is totally ordered) there is a gayest human. Edit:though they may not necessarily be unique.
There are more than 0 people currently the gayest.
I thought Smith won most gay?
"Being gay isn't a choice, it's a competition. And I'm winning."
Gay Olympics when?
What would gay Olympics look like? Like this?