Infinity gangsta when aleph null walks in

What about infinity times zero?

Quaternions hello?

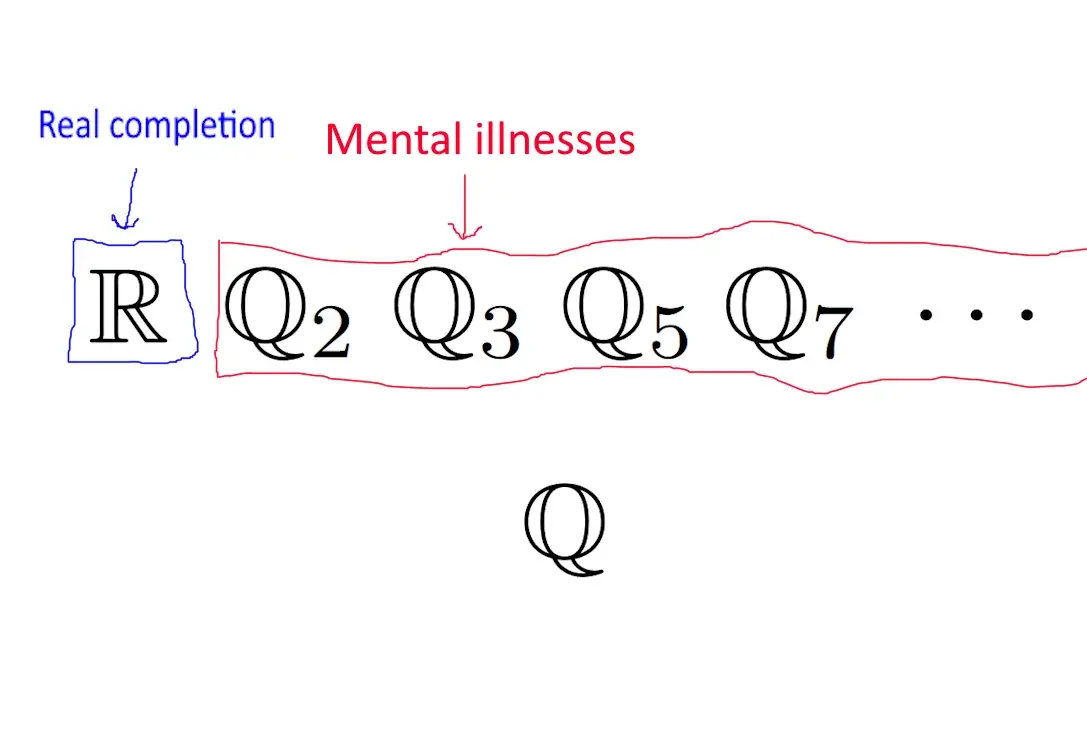
This image goes so hard

Wait, they ran out of greek letters and started using Hebrew ones now? When did that happen?

Which of the infinities? There are many, many :D

Oh no! Please don't tell me there are infinity infinities!

Hi, I'm a mathematician. My specialty is Algebra, and my research includes work with transfinites. While it's commonly said that infinity "isn't a number" I tend to disagree with this, since it often limits how people think about it. Furthermore, I always find it odd when people offer up alternatives to what infinity is; are numbers never concepts?

Regardless, here's the thing you're actually concretely wrong about: there are provably things bigger than infinity, and they are all bigger infinities. Furthermore, there are multiple kinds of transfinite algebra. Cardinal algebra behaves mostly like how you described, except every transfinite cardinal has a successor (e.g. There are countably many natural numbers and uncountably many complex numbers). Ordinal algebra, on the other hand, works very differently: if ω is the ordinal that corresponds to countable infinity, then ω+1>ω.

You have the spirit of things right, but the details are far more interesting than you might expect.

For example, there are numbers past infinity. The best way (imo) to interpret the symbol ∞ is as the gap in the surreal numbers that separates all infinite surreal numbers from all finite surreal numbers. If we use this definition of ∞, then there are numbers greater than ∞. For example, every infinite surreal number is greater than ∞ by the definition of ∞. Furthermore, ω > ∞, where ω is the first infinite ordinal number. This ordering is derived from the embedding of the ordinal numbers within the surreal numbers.

Additionally, as a classical ordinal number, ω doesn't behave the way you'd expect it to. For example, we have that 1+ω=ω, but ω+1>ω. This of course implies that 1+ω≠ω+1, which isn't how finite numbers behave, but it isn't a contradiction - it's an observation that addition of classical ordinals isn't always commutative. It can be made commutative by redefining the sum of two ordinals, a and b, to be the max of a+b and b+a. This definition is required to produce the embedding of the ordinals in the surreal numbers mentioned above (there is a similar adjustment to the definition of ordinal multiplication that is also required).

Note that infinite cardinal numbers do behave the way you expect. The smallest infinite cardinal number, ℵ₀, has the property that ℵ₀+1=ℵ₀=1+ℵ₀. For completeness sake, returning to the realm of surreal numbers, addition behaves differently than both the cardinal numbers and the ordinal numbers. As a surreal number, we have ω+1=1+ω>ω, which is the familiar way that finite numbers behave.

What's interesting about the convention of using ∞ to represent the gap between finite and infinite surreal numbers is that it renders expressions like ∞+1, 2∞, and ∞² completely meaningless as ∞ isn't itself a surreal number - it's a gap. I think this is a good convention since we have seen that the meaning of an addition involving infinite numbers depends on what type of infinity is under consideration. It also lends truth to the statement, "∞ is not a number - it is a concept," while simultaneously allowing us to make true expressions involving ∞ such as ω>∞. Lastly, it also meshes well with the standard notation of taking limits at infinity.

That regex implies “” is a number

I didn't realize '.' is a number.

\([0-9]+\.[0-9]\)?[0-9]* is more accurate I think.

But those are parentheses, are they not? I was taught intervals using square brackets and semicolon. While parentheses are used for coordinates and tuples. The square brackets indicates inclusion of the boundary number.

Ie. the statement "2

Update: apparently either lemmy or my app (boost) wasn't that excited for my less than signs, and just skipped the rest of the comment. And here I had spent time copying both "less than or equal to" and infinity signs, since my keyboard doesn't seem to have them... For the time being pls disregard the comment above, while I figure out how to write math on lemmy.