was about to fall asleep but then PROPOSITION:
- all magic squares are constant multitles (all numbers multiplied by a certain value), or shifted (all numbers added to by a certain value) of a very few variations of "base" magic squares this seems intuitively true by a sleepy deprived person at 1am, but if we can prove for these "base" squares, would that be the way to prove for the general case?
i.e. there r and infinite number of 1x1 magic squares, but there is only one case to deal with if we want to prove anytning about it
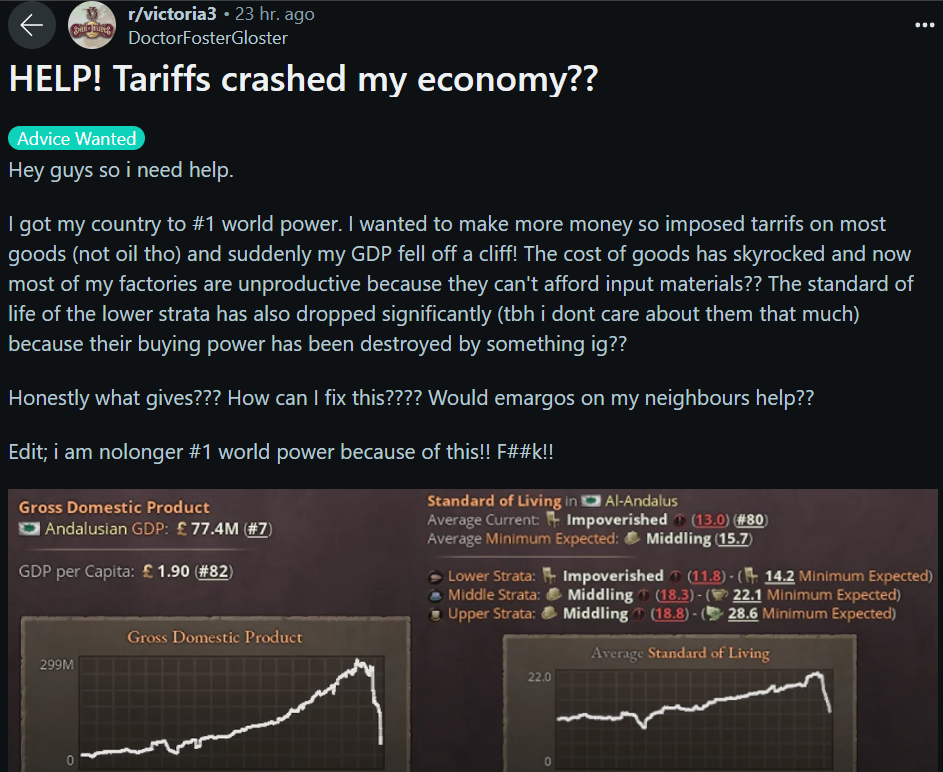





what about this square, it does not have an inverse