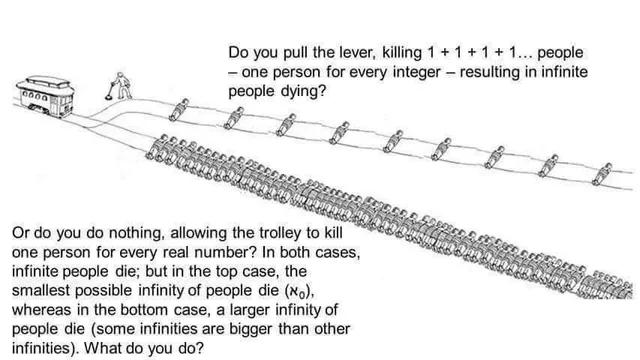
Multi-track drifting. Also while some infinities are smaller if you're just counting out an infinite number of individual humans then I'm pretty sure they're the same size infinities one is just social distancing. Smaller infinities are ones like those in between each part of the bigger infinities. To represent a smaller infinity you'd maybe have to have an infinite number of smaller humans crammed into a spot the size of one of the spaces between the humans on the other track, or something along those lines. The real number track does contain smaller infinities between each integer via infinite decimal points but I don't think one track would technically be smaller than the other in this case since they run parallel to each other but neither are technically limited in the "length" of their infinity so to speak. But I could be misremembering how they classify smaller infinities.
Science Memes
Welcome to c/science_memes @ Mander.xyz!
A place for majestic STEMLORD peacocking, as well as memes about the realities of working in a lab.

Rules
- Don't throw mud. Behave like an intellectual and remember the human.
- Keep it rooted (on topic).
- No spam.
- Infographics welcome, get schooled.
This is a science community. We use the Dawkins definition of meme.
Research Committee
Other Mander Communities
Science and Research
Biology and Life Sciences
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- !reptiles and [email protected]
Physical Sciences
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
Humanities and Social Sciences
Practical and Applied Sciences
- !exercise-and [email protected]
- [email protected]
- !self [email protected]
- [email protected]
- [email protected]
- [email protected]
Memes
Miscellaneous
Pull the switch as the trolley is on that rail so it gets stuck and the trolley kills nobody
The same thing most people would do when presented with a Trolly Problem for real. Analysis paralysis, choose to do nothing, then cry softly every night for the rest of my life.
Gödel posse represent!
Infinity cannot be divided, if it can then it becomes multiple finite objects. Therefore there cannot be multiple Infinities. If infinity has a size, then it is a finite object. If infinity has a boundary of any kind, then it is a finite object.
Infinity cannot be divided, if it can then it becomes multiple finite objects.
It really depends on what you mean by infinity and division here. The ordinals admit some weaker forms of the division algorithm within ordinal arithmetic (in particular note the part about left division in the link). In fact, even the cardinals have a form of trivial division.
Additionally, infinite sets can often be divided into set theoretic unions of infinite sets fairly easily. For example, the integers (an infinite set) is the union of the set of all integers less than 0 with the set of all integers greater than or equal to 0 (both of these sets are of course infinite). Even in the reals you can divide an arbitrary interval (which is an infinite set in the cardinality sense) into two infinite sets. For example [0,1]=[0,1/2]U[1/2,1].
Therefore there cannot be multiple Infinities.
In the cardinality sense this is objectively untrue by Cantor's theorem or by considering Cantor's diagonal argument.
Edit: Realized the other commenter pointed out the diagonal argument to you very nicely also. Sorry for retreading the same stuff here.
Within other areas of math we occasionally deal positive and negative infinities that are distinct in certain extensions of the real numbers also.
If infinity has a size, then it is a finite object.
Again, this is not really true with cardinals as cardinals are in some sense a way to assign sizes to sets.
If you mean in terms of senses of distances between points, in the previous link involving the extended reals, there is a section pointing out that the extended reals are metrizable, informally this means we can define a function (called a metric) that measures distances between points in the extended reals that works roughly as we'd expect (such a function is necessarily well defined if either one or both points are positive or negative infinity).