Science Memes

11440 readers

1307 users here now

Welcome to c/science_memes @ Mander.xyz!

A place for majestic STEMLORD peacocking, as well as memes about the realities of working in a lab.

Rules

Don't throw mud. Behave like an intellectual and remember the human.
Keep it rooted (on topic).
No spam.
Infographics welcome, get schooled.

This is a science community. We use the Dawkins definition of meme.

Research Committee

[email protected]

Other Mander Communities

Science and Research

Biology and Life Sciences

Physical Sciences

Humanities and Social Sciences

Practical and Applied Sciences

Memes

Miscellaneous

founded 2 years ago

MODERATORS

[email protected]

908

hmmmm (mander.xyz)

submitted 10 months ago by [email protected] to c/[email protected]

194 comments fedilink hide all child comments

you are viewing a single comment's thread
view the rest of the comments

[–] [email protected] 1 points 9 months ago (1 children)

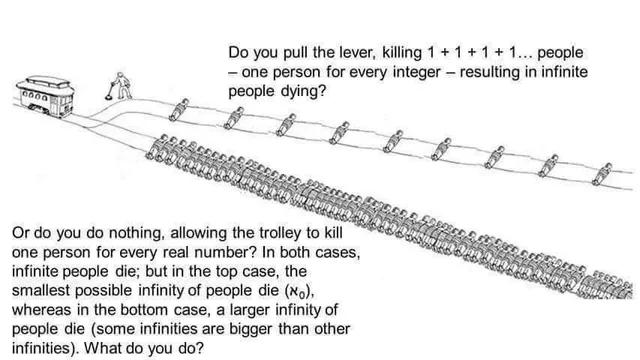
Was this an honest question? Because the answer is 'no'. You can't space them out or else the set of people on the lower track would be countable which is a smaller infinity than the ones of the real numbers.

To space them, you would have to take people of the track. Infinitely many. To be precise not all of them but as many as there are on the track.

[–] [email protected] 1 points 9 months ago

@EunieIsTheBus @science_memes It was half joke, half paradox. 😁

If you kill two sets at the same rate, but one set is smaller, is it less bad?

The set with one person for every real number, they're neither spaced nor adjacent. It's kind of a Zeno's paradox scenario: no person can ever be first, next, or last. So I think if we can set the rate of killing the same, I'll choose the real numbers track in hopes that the trolley can't ever begin. If we set the rate at speed down the track, it's gotta be the integers.