Science Memes

11441 readers

1417 users here now

Welcome to c/science_memes @ Mander.xyz!

A place for majestic STEMLORD peacocking, as well as memes about the realities of working in a lab.

Rules

Don't throw mud. Behave like an intellectual and remember the human.
Keep it rooted (on topic).
No spam.
Infographics welcome, get schooled.

This is a science community. We use the Dawkins definition of meme.

Research Committee

[email protected]

Other Mander Communities

Science and Research

Biology and Life Sciences

Physical Sciences

Humanities and Social Sciences

Practical and Applied Sciences

Memes

Miscellaneous

founded 2 years ago

MODERATORS

[email protected]

908

hmmmm (mander.xyz)

submitted 10 months ago by [email protected] to c/[email protected]

194 comments fedilink hide all child comments

you are viewing a single comment's thread
view the rest of the comments

[–] [email protected] 0 points 10 months ago (1 children)

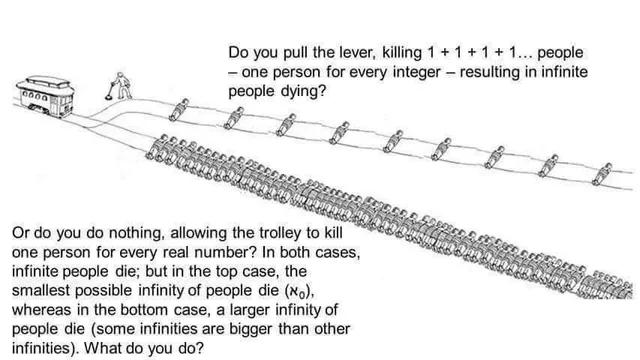
The set, that has a measurable starting point, is a finite object. If infinity can be measured, then you have created a finite space, one that can be measured, within an infinite space, infinity itself, which cannot be measured. Infinity remains untouched and undivided. The sets that represent infinity are finite objects, that represent an infinite space, a representation which they can never truly achieve.

[–] [email protected] 2 points 10 months ago

Maybe we should talk about what "infinite" means. I'd like to propose the following idea: a sequence of things is infinite, if there is always "one more" object to consider. We could also say that for any number of finite steps, there is always another object of the series we haven't looked at yet.

As an example, the sequence of natural numbers would satisfy this: if I start considering the sequence 1, 2, 3 and so on, if I ever stop after finite time (say 1729 steps), I can always compute +1 to find another element of the sequence I haven't seen yet.

Also consider the following: the set of all numbers between 0 and 1 is in some sense bounded. However, I can find an infinite sequence of numbers in this set: consider 1/1, 1/2, 1/3, 1/4, ...

These numbers are always between 0 and 1, and are infinitely decreasing.

Perhaps the confusion comes from you talking about infinity as in a number which is larger than any real or natural number, while I'm talking about sizes of sets of infinite size. As I had demonstrated earlier, we can show the existence of uncountable infinite vs countably infinite sets, while such distinctions don't really come up in limit theory and calculus.