Daily Maths Challenges

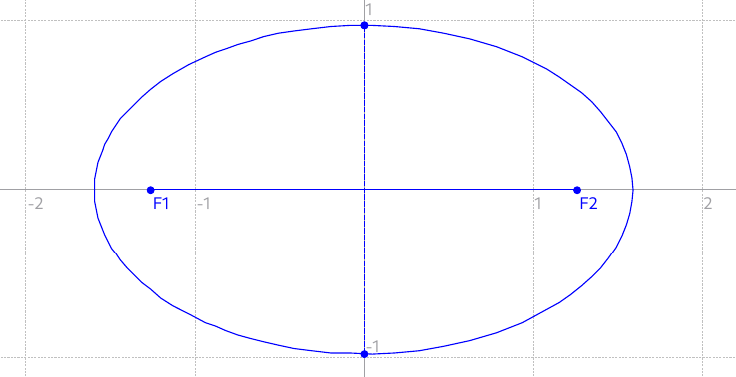
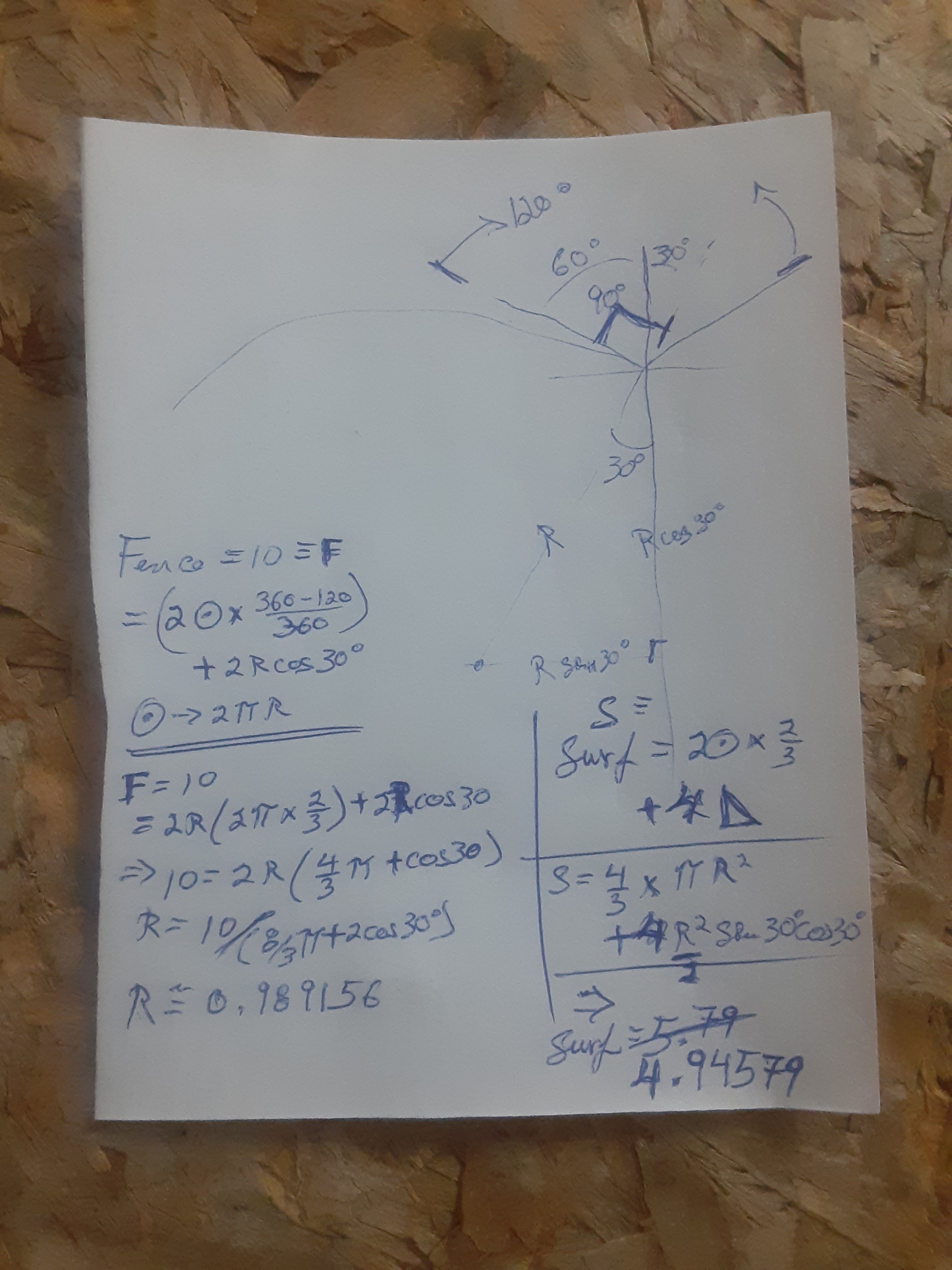
Here's another solution, that is suboptimal but might be preferable to the soap bubble solution in practice: an ellipse with long axis 1.592 and short axis 0.972. This should be close to the optimal ellipse (I used Kepler's approximate P=pi * (a+b) formula for the perimeter). It gives an area of 4.861 which is close enough to the current optimum, and looks like this:

it's like the shape of two soap bubble touching : at every point where three walls meet there is three times 120°

Nice Problem you got there. I am not really in a mood to do functional calculus, but this question is a functional calculus question. I will try to give the setup, but not going to solve it (sorry, getting sleepy).

with some clever symmetry arguments, the fence should be symmetric about a line (or plane) bisecting the 2 rabbits, and since we have to also create a wall there, we have to have a line, somewhere in this plane

now we can consider a parametric form for equation of fence.

if you are unaware of functional calculus, it is a very fun branch of calculus, where instead of maximising value of a variable, we maximise a "function" it self. for a readup, refer https://en.wikipedia.org/wiki/Action_(physics)#Hamilton's_characteristic_function https://en.wikipedia.org/wiki/Euler%E2%80%93Lagrange_equation

To solve, we need a constant (or a constraint, in this case total fence length), and a function which we want to extremise (in this case, maximise the area of enclosed by fence).

to keep the problem simple, lets consider, a single valued function (f(x) -> y) (for a general proof, we can do f(x, y) -> z), and also consider some dividing segment, now lets consider the leftmost and rightmost extremes to have values +/- alpha (assuming symmetry in this direction also, not necessary to assume this, but doing for simplicity), now we have a straight fence between some section of these extremes (lets say +/- beta) now total length of fence is constant so

10 = 2 beta + twice (line integral from - alpha to + alpha of f(x))

(line integral is not same as usual integral, you may also know it by name of path integral)

this gives us a constraint

now we can find area enclosed by

twice (integral from - alpha to + alpha f(x) dx )

now use the Euler - Lagrange equation to find a solution for f(x)

this is a very general way to find the solution, and this will also mathematically prove that our solution is the best. If you are also not interested in doing maths, you can use some llm (like chatgpt) to formally setup the problem for you, and then you can use some solver like wolfram alpha to get solution.

The best I was personally able to obtain is the circle divided by a wall.

I initially asked this question on the mathematics stack exchange: https://math.stackexchange.com/questions/5035579/area-maximization. Of course, it got closed for no reason, but before it did, someone offered the following solution: join two circular arc (subtended at angle 240∘ with respect to their center) at their end points, add a line segment between the end points, you can achieve an area ∼4.9457788. Recomputing the area of their solution, I get ~4.49 instead, but I'm not sure I got it right...

Does the entire boundary have to be made of the mesh? Especially relevant if this is for practical use rather than just a challenge since you could use e.g. two existing corners in a rectangular yard: cut the mesh in half, and use 5m to close off each corner. Making isosceles triangles out of each corner with the two equal length sides having length sqrt(25/2) ~= 3.535m gives areas of 6.25 sq. meters for each rabbit.

You could do even better if you happened to already have 3 walls of the appropriate lengths to partition off an area in as well... e.g. 2.5m x 5m = 12.5 sq m. for each rabbit if you have a rectangular yard surrounded by an existing wall where the back wall is 5m long and the other two sides are at least 2.5m long. That configuration is less likely for someone to already actually have though.