this post was submitted on 29 Sep 2023
1476 points (95.8% liked)
Memes
46492 readers
820 users here now
Rules:
- Be civil and nice.
- Try not to excessively repost, as a rule of thumb, wait at least 2 months to do it if you have to.
founded 5 years ago
MODERATORS
you are viewing a single comment's thread
view the rest of the comments
view the rest of the comments
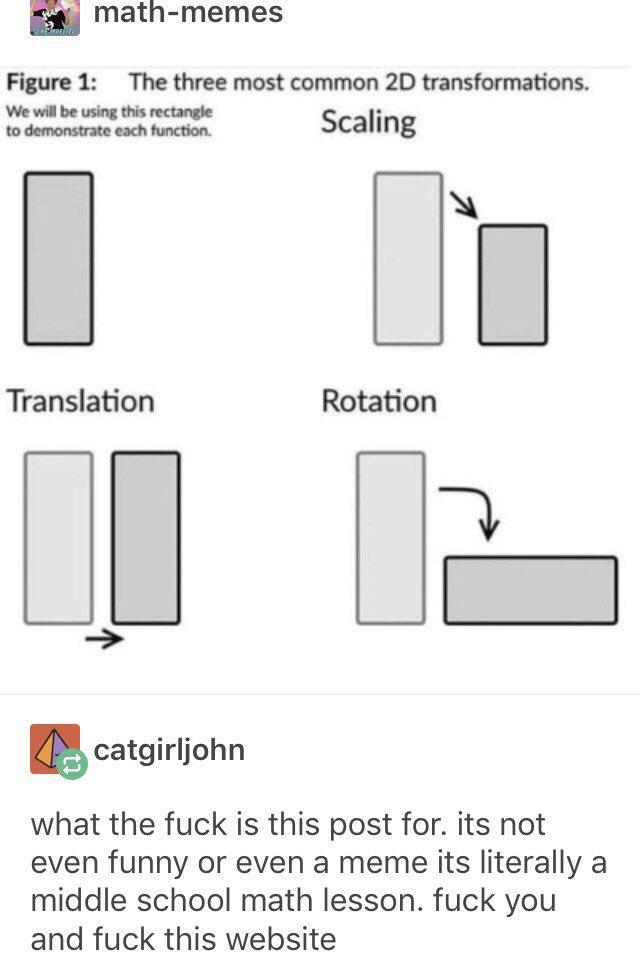
R e a l l y?
I believe you, but what do I need to read to understand why that is?
There are many ways to prove it but my preferred one is by using complex numbers. In what follows we identify 2D points and vectors with their complex representation so that we won't have to deal with too many notations.
Let there be three points
z,z'andz'', and assume that:z'is obtained fromzby applying a rotation of angleθand centeru;z''is obtained fromz'by applying a translation byv.That means that we have:
z' - u = (z - u) * exp(i * θ)z'' = z' + vIn particular, we have:
z'' = u + v + (z - u) * exp(i * θ)It kinda looks like a rotation is there, since we have a
exp(i * θ), so we'd ideally like to have the right-hand side in the above equality be in the formw + (z - w) * exp(i * θ).Let's see if we can achieve that, we'll look for
wsuch that:w + (z - w) * exp(i * θ) = u + v + (z - u) * exp(i * θ)Which after some simplifications becomes:
w * (1 - exp(i * θ)) = u * (1 - exp(i * θ)) + vAnd assuming that
θis not a multiple of2 * pi, we can divide both sides by1 - exp(i * θ)and we get:w = u + v / (1 - exp(i * θ))(from here you can easily further simplify to get the explicit 2D coordinates ofw)So what we've shown is that there indeed exists a unique center
wsuch thatz''is obtained fromzby applying a rotation of angleθaroundw, ie:z'' - w = (z - w) * exp(i * θ)