this post was submitted on 15 May 2024
19 points (100.0% liked)
Daily Maths Challenges
208 readers
1 users here now
Share your cool maths problems.
Complete a challenge:
- Post your solution in comments, if it is exactly the same as OP's solution, let us know.
- Have fun.
Post a challenge:
- Doesn't have to be original, as long as it is not a duplicate.
- Challenges not riddles, if the post is longer than 3 paragraphs, reconsider yourself.
- Optionally include solution in comments, let it be clear this is not a homework help forums.
- Tag [unsolved] if you don't have a solution yet.
- Please include images, if your question includes complex symbols, attach a render of the maths.
Feel free to contribute to a series by DMing the OP, or start your own challenge series.
founded 9 months ago
MODERATORS
you are viewing a single comment's thread
view the rest of the comments
view the rest of the comments

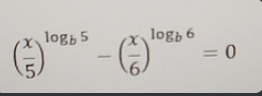
Yes, though I prefer spoilered answers with work (especially since something like Wolfram|Alpha can just spit out the answer here)
I'm curious about your retracted edit, since I saw your original message had just the correct answer - why 30k?
I thought 0 also works so maybe it's multiples of 30 but then tried 60 and it didn't work
spoilers
0 does work as a trivial solution, since 0^a = 0^b always holds, but yea, 30's the only other one - the key comes down to the fact that a^log(b) = b^log(a) in general, and 30 is what achieves that herei get why 0 would work, but i dont get how it doesnt show up as a solution when i try to solve for it
In your own work, you divided by x^ln(6) at one point, which would remove any x = 0 solution from your work - before that step x = 0 was still a valid solution to your equations, but after it it wasn't
Expanding on my reply, here's a different way to continue your own work that would have yielded both solutions, by avoiding any steps that divide by x:
solution
Starting from the third line of your work:(x/5)^ln(5) = (x/6)^ln(6)
x^ln(5) / 5^ln(5) = x^ln(6) / 6^ln(6) → Distribute exponents
x^ln(5) * 6^ln(6) - x^ln(6) * 5^ln(5) = 0 → Cross multiply, move terms to one side
x^ln(5) * (6^ln(6) - x^ln(1.2) * 5^ln(5)) = 0 → Factor out x^ln(5)
Can set each factor to 0:
x^ln(5) = 0 yields x = 0
6^ln(6) - x^ln(1.2) * 5^ln(5) = 0
6^ln(6) / 5^ln(5) = x^ln(1.2) → Add right term to right side, divide by its coefficient
(5^(ln(6)/ln(5)))^ln(6) / 5^ln(5) = x^ln(1.2) → Convert numerator of left side to have same base as denominator, using change of base formula: log_5(6) = ln(6)/ln(5)
5^(ln(6)^2 / ln(5)) / 5^ln(5) = x^ln(1.2) → Simplify exponent of numerator slightly
5^((ln(6)^2 - ln(5)^2) / ln(5)) = x^ln(1.2) → Combine terms on left side, simplify numerator into a single fraction
5^((ln(6)+ln(5))(ln(6)-ln(5))/ln(5)) = x^ln(1.2) → Factor exponent numerator as difference of squares
5^(ln(30)ln(1.2)/ln(5)) = x^ln(1.2) → Simplify sum and difference of logs in left exponent numerator
30^ln(1.2) = x^ln(1.2) → By change of base formula again, ln(30)/ln(5) = log_5(30), so 5^(ln(30)/ln(5)) = 30
x = 30