I'm interested, how else would you find the solution besides plugging in a guess and adjusting up or down until it works?
this post was submitted on 11 Nov 2023
4 points (83.3% liked)
Riddles
261 readers
1 users here now
Answer these riddles and the esophagus will let you pass.
Riddles for 'Lemmy'winks.
founded 2 years ago
MODERATORS
I think it'd have multiple solutions so it'd just be an algebraic formula right?
x.(y-5) = 2(y.x)
solve for x, plot graph, pick positions where both x and y stop at the hundredths column.
been a minute since over had to think about this stuff so maybe did that wrong lol
Yeah, it's been too long for me too. I came up with the same first formula, was looking at it not really wanting to solve for X or try to find my graphing calculator when I realized it still wouldn't land just on appropriate solutions, and wondered if there was a better way. But once it is graphed, yeah, finding where the solutions don't go past the hundredths column works.
Your response also made me think of looking for a graphing calculator app again. I did once a frightening number of years ago and didn't find much and I never thought of it again, haha!
If x is the dollar amount written on the check and y is the cents amount.
The original check amount was: x+y
The amount that teller handed the lady was: 100y+x/100
The amount the lady found in her bag was: 100y + x/100 - 0.05
We know the lady found twice the amount of the original check: 2(x+y) = 100y + x/100 - 0.05
They want you to solve for the original check amount x+y.
I messed up my algebra somewhere because I got: x=(5+9800y)/199 which if you set y = 0.63 you get x = 31.05 so I'm off somewhere.
I wasn't too far off, I dropped a minus sign somewhere.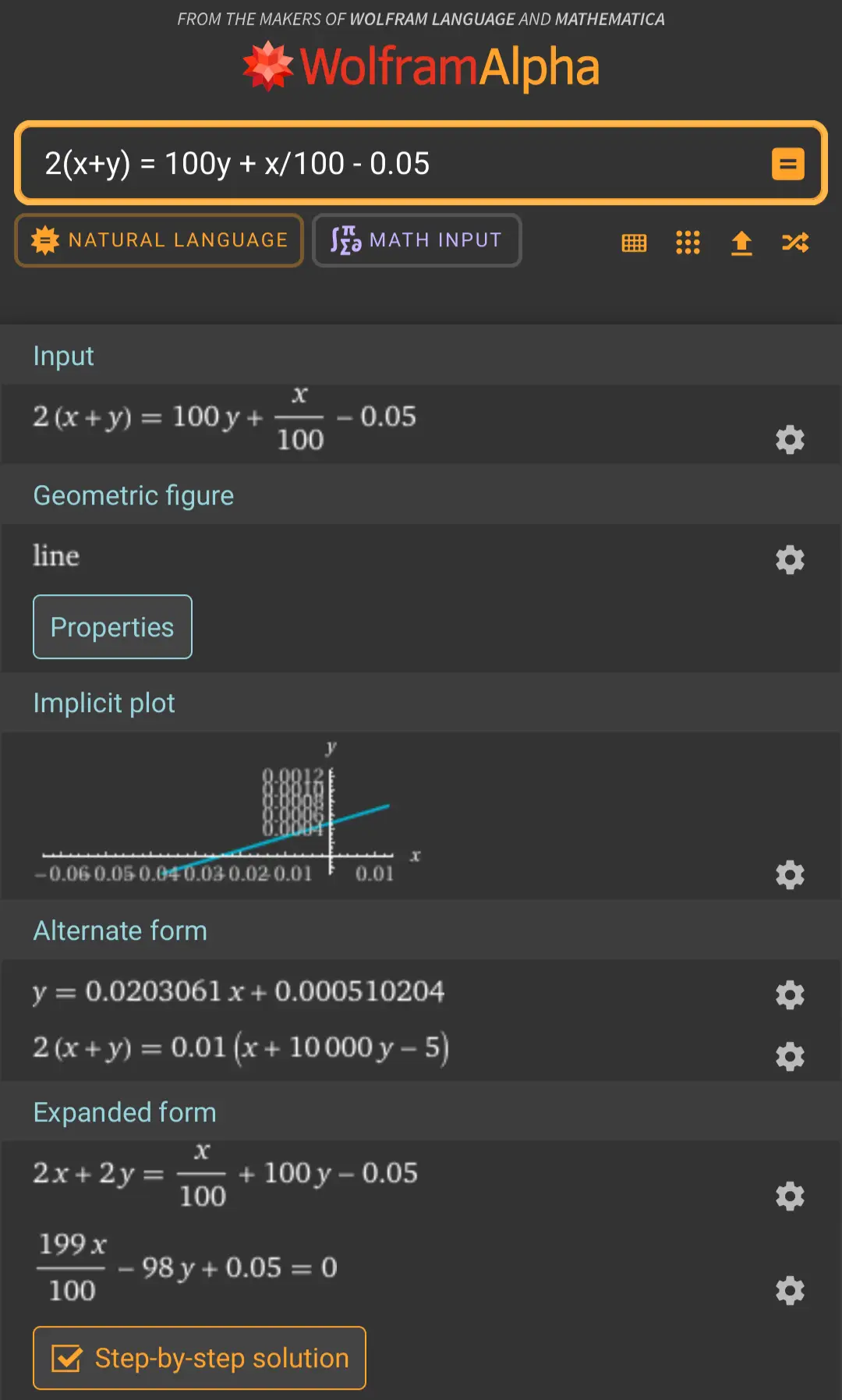 
I can't think of a mathematical way to constrain x to be positive integers and constrain y to be any integer 0 to 99 divided by 100. Using a graph was a good idea