General community for all things mathematics on @lemmy.world
Submit link and text posts about anything at all related to mathematics.
Questions about mathematical topics are allowed, but NO HOMEWORK HELP. Communities for general math and homework help should be firmly delineated just as they were on reddit.
I understand that 1/10 is a lot more than 1/1000, so obviously some of the highest percentages will be attributed to the smaller apps. However, when it comes to ranking these apps, do I go by 5-star reviews? 1-star reviews? The ratio of reviewers to downloaders? How would you go about this?
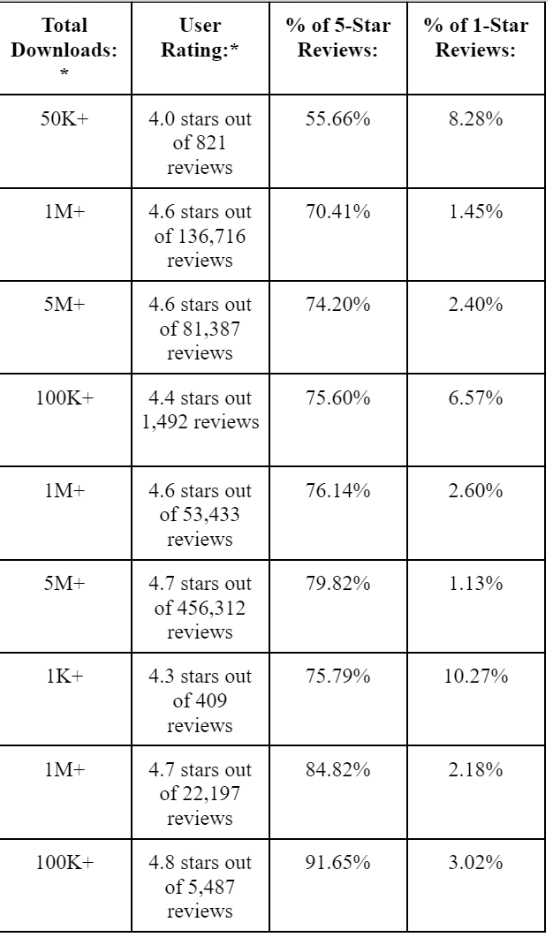
It depends on what the app is for I think. For apps that just need to work (I can't afford it to break at a bad time), the most important thing is that it's well tested (lots of downloads) and has few 1 star reviews. I'd probably thus require 1M+ downloads (or perhaps 100k), and then rank those by % of downloads that result in 1 star reviews. That is: take the number of reviews, multiply by % 1 star, and divide that by number of downloads. (I assume that if someone has a 'necessary' app break, they will leave a review. This might be false if someone is using bots to inflate download numbers)
Interesting take.
I thought about the equation of (r/d) * p = x, r = total reviews, d = total downloads, p = percentage of 1-star reviews, and x = rank value, but the download amount is approximate.