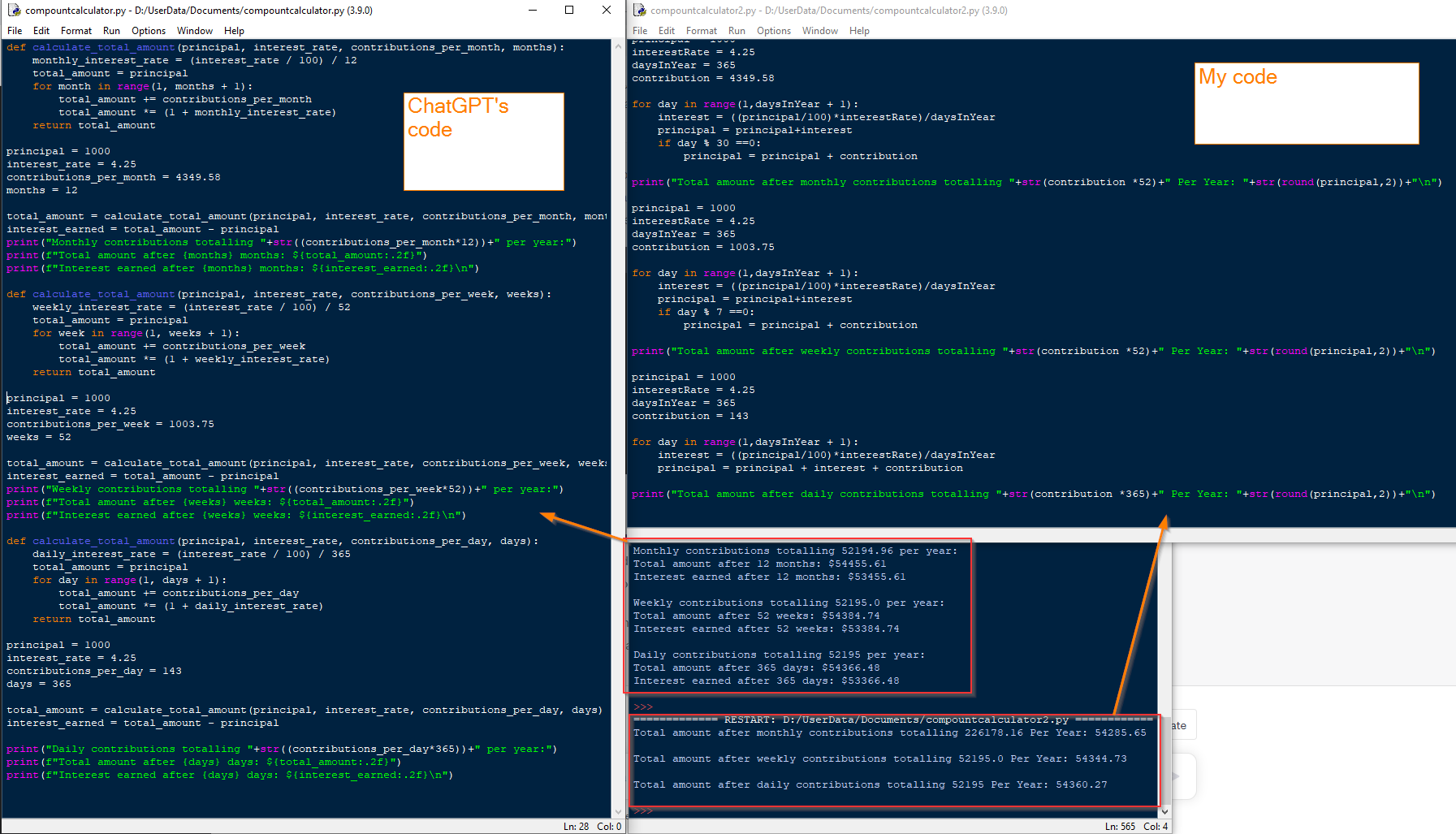
Without starting to calculate, or looking at the code, I'd say it's obvious that an investment strategy where all of a month's contributions are made on the first day of the month will be superior to one where you spread them out. Also, an investment strategy of making the month's contributions on the last day will be inferior to spreading them.
So it'd really depend on how you time your monthly investments. If you can invest as soon as you get your monthly income, that's probably the most beneficial way to do it.
edit — Taking a quick look at your code, that's exactly what's happening. In each period, ChatGPT invests first, then lets interest accrue, whereas you let interest accrue, then invest.