Comic Strips

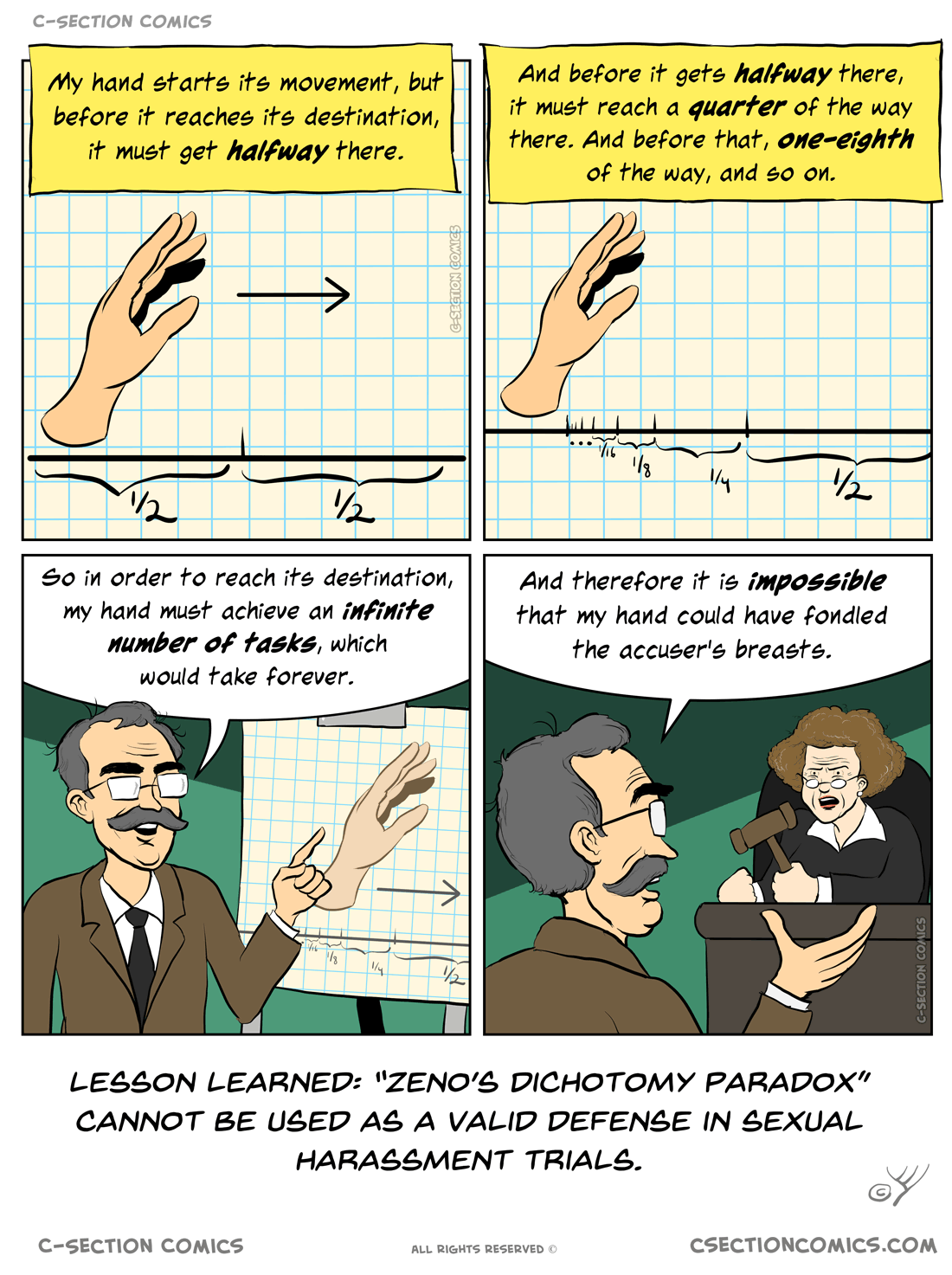
Not that anyone cares but I just realized that this is not actually paradoxical and I can prove it mathematically! (I think) Bear with me since I’ve like just barely learned this stuff this week.

Proof Let S be the set of all steps needed to be taken. It can be written as S = {(distance to be traveled)(2^-n^): n in the Natural numbers}. Thus, S shares cardinality with the natural numbers and is countably infinite.

However, time is continuous. Thus, it has the cardinality of the continuum (real numbers) which means any time interval contains an uncountably infinite amount of moments. Let us denote an arbitrary time interval as T.

Because | T | > | S | there is no injection from T to S. Thus if each step has only 1 time value, there will be moments of time left over, and since the hand is not in two places at once we know each step must have its own time value, so this must be the case.

Therefore, when moving in steps like this, one will run out of infinite steps before they run out of moments in time to complete those steps. Hence, any finite distance can be traversed in this way over some bounded interval of time. QED.

Basically, you can traverse any distance in any time interval as long as physics allows you to move at a fast enough speed. Even if it doesn’t, there may be a limit to how fast you can traverse the distance, but it is still bounded. You can traverse any finite distance like this before existence runs out of time.

(I’m still learning. So if there’s an error in my proof please be gentle lol)